Zipf’s Law in Passwords

Abstract

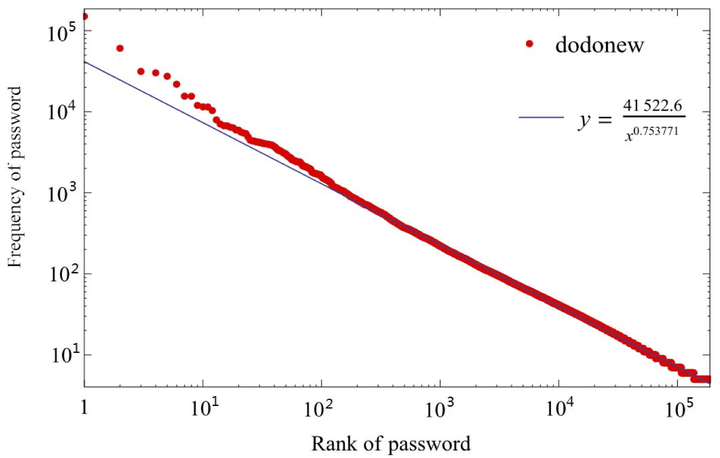
Despite three decades of intensive research efforts, it remains an open question as to what is the underlying distribution of user-generated passwords. In this paper, we make a substantial step forward toward understanding this foundational question. By introducing a number of computational statistical techniques and based on 14 large-scale data sets, which consist of 113.3 million real-world passwords, we, for the first time, propose two Zipf-like models (i.e., PDF-Zipf and CDF-Zipf) to characterize the distribution of passwords. More specifically, our PDF-Zipf model can well fit the popular passwords and obtain a coefficient of determination larger than 0.97; our CDF-Zipf model can well fit the entire password data set, with the maximum cumulative distribution function (CDF) deviation between the empirical distribution and the fitted theoretical model being 0.49%~4.59% (on an average 1.85%). With the concrete knowledge of password distributions, we suggest a new metric for measuring the strength of password data sets. Extensive experimental results show the effectiveness and general applicability of the proposed Zipf-like models and security metric.